goormNLP [Regularization]

Auspice by Goorm, Manage by DAVIAN @ KAIST

Lecture: Regularization

2022-01-27

Regression에 적용할 수 있는 Regularization 방법에 대한 이론 및 실습을 진행하였다.

과거 프로젝트를 진행했었을 때 그저 학습이 좋아지게 한다는 도구로써 사용했던 Regularization을 세세하게 이해하였고

다음 프로젝트 및 Competition에 적용하여 더 좋은 점수를 나오게 진행을 해봐야겠다…

The problem of overfitting

Addressing overfitting:

1. Reduce number of features.
   • Manually select which features to keep.
   • Model selection algorithm.
2. Regularization
   • Keep all the features, but reduce magnitude/values of parameters.
   • Works well when we have a lot of features, each of which contributes a bit to predicting $y$.

Cost function

기존에 있는 cost function에 regularization parameter를 추가하고, λ의 value를 조정하여 overfitting과 underfitting을 탈출함.

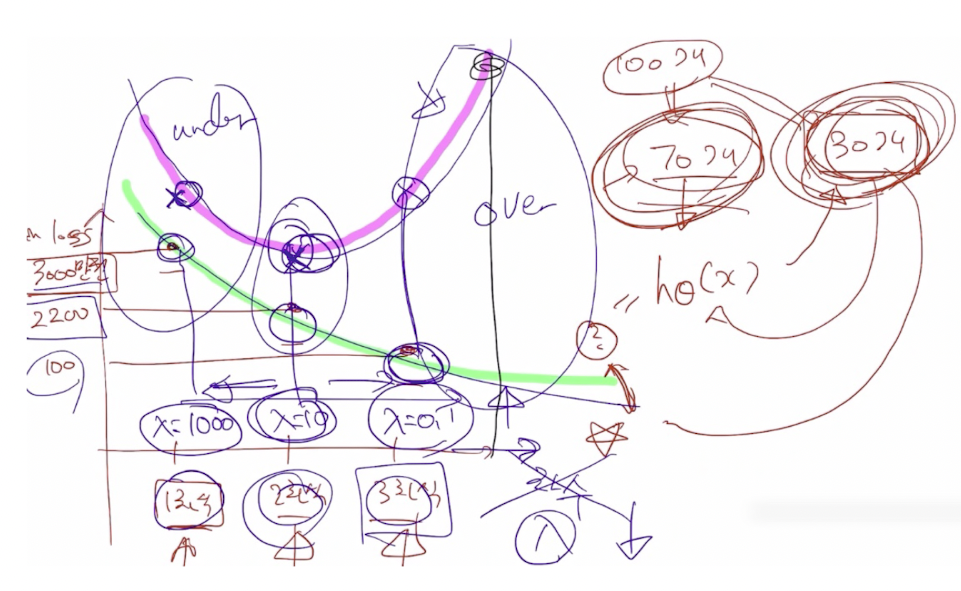
λ의 value가 크면 underfit, λ의 value가 작으면 overfit이 됨.

Practice

지난 practice에서는 Linear / Rogistic regression에 대해서 알아보았다.

이번에는 Polynomial regression과 Regularization을 실습을 통해 알아볼 것이다.

1. 4차 polynomial function: $y = x^4 + x^3 - 4x^2$ 을 이용해서 데이터를 생성함.

2. $d$ 차 곡선을 정의하고 polynomial regression 또한 multiple linear regression 문제와 동일하기 때문에, 아래의 행렬처럼 나타낼 수 있음.

$\hat{y} = w_0 + w_1x + w_2x^2 + … + w_dx^d$

3. 데이터들을 MinMaxScaler하고, 모델 (3차 항)을 훈련한 결과, 아래와 같이 잘 훈련된 결과가 plot 됨.

4. 3차 항의 모델이 아닌 1차 항과 15차 항 모델을 훈련한 결과, 아래와 같이 plot 됨.

1차 항의 결과, 직선은 너무 간단해서 데이터가 흩뿌려져 있을 때는 그 데이터를 잘 설명하지 못함.
이것은 underfitting 되었다고 할 수 있음.

==> high bias(정답에서 멀음), low variance(한 군데에 모여있음)

15차 항의 결과, Training data를 모두 커버하려고 매우 복잡한 모델이 되기 때문에, Test data를 잘 못 맞추게 됨.
이것은 overfitting 되었다고 할 수 있음.

==> low bias(정답에서 가까움), high variance(한 군데에 모여있지 않음)

5. Regularization

regularization term 인 $\lambda\sum_{j=1}^dw_j^2$를 추가하고,. Mean-squared error를 사용한 cost function에 추가하면 다음과 같다..

$L(\mathbf{w}) = \frac{1}{N} \lVert \mathbf{y} - \mathbf{Xw} \rVert^2 + \lambda \sum_{j=1}^d w_j^2$

새롭게 만든 cost function은 계수들이 작은 값이 되는 것을 선호하게 됨. 계수들이 커지게 되면 두번째 항이 커지게 돼서 cost 값이 늘어나기 때문.

λ는 regularization paramter이며 얼마나 큰 제약을 줄 것인가를 결정함. λ가 큰 값을 가질수록 계수들을 더 작게 할 수 있음.
이번 practice에서는 λ의 값을 1로 설정함.

Regularization의 결과, 15차 항에서 예측 모델이 진동하는 것이 아닌 부드럽게 학습 데이터들을 지나가는 것을 볼 수 있음.
이렇게 된다면 새롭게 들어오는 데이터도 잘 예측할 수 있게 됨.

---

HW13 링크