goormNLP [Logistic Regression]

Auspice by Goorm, Manage by DAVIAN @ KAIST

Lecture: Logistic Regression

2022-01-26

지금까지 주어진 데이터와 가장 잘 맞는 직선을 찾는 Linear Regression을 진행했었다.

이번에는 예측 값이 연속적인 값을 갖지 않는 Logistic Regression에 대해서 알아볼 것이다.

Classification

Logistic function

Logistic regression을 진행하기 위해서는 출력 값을 0과 1의 값으로 맞춰주어야 한다.

이를 위해서 logistic function 을 사용했고, Logistic function은 아래와 같다.

$\sigma(z) = \frac{1}{1 + e^{-z}}$

Logistic regression을 진행할 때 입력 데이터를 $x$, 실제 class 값을 $y$, 예측된 출력 값을 $\hat{y}$라고 하면 $x$는 두가지 변환을 거쳐서 $\hat{y}$가 된다.

$z = wx + b$ $\hat{y} = \sigma(z)$

위에 있는 식의 목표는 $\hat{y}$가 실제 $y$와 가장 가깝게 되도록 하는 $w$와 $b$를 찾는 것 이다.

Logistic loss function

$\sigma(z) = \frac{1}{1 + e^{-z}}$

$\sigma’(z) = \sigma(z) ( 1 - \sigma(z))$

$\frac{\partial{L}}{\partial{\sigma(z)}} = \frac{(y-\sigma(z))}{\sigma(z)(1-\sigma(z))}$

위와 같은 과정을 통해 구한 cost function $L$은 $L = -y \log(a) + (y-1)\log(1-a)$이 된다.

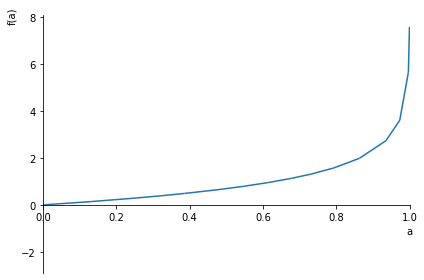
만약 $y=1$이라면 $L = -\log(a)$만 남게 되며, 그래프로 표현하면 다음과 같다.
실제 class가 1일때 예측 값이 0에 가까워지면 cost function 값이 커지고, 1에 가까워지면 cost function 값이 작아지는 것을 알 수 있다.

이제 $y=0$이라면 $L = \log(1-a)$ 만 남게 되며, 그래프로 표현하면 다음과 같다.
예측 값이 실제 값이랑 가까워지면 cost function 값이 작아지고 멀어지면 커지게 됨을 알 수 있다.

Practice

빨간색 곡선이 Logistic Regression의 모델이다.
기준값을 정한 후, 그것보다 크면 1, 작으면 0으로 분류를 진행하게 된다.
아래 사진은 기준값을 0.5로 설정한 예시이다.

---

HW12 링크