goormNLP [Advanced Eigendecomposition (1)]

Auspice by Goorm, Manage by DAVIAN @ KAIST

Lecture 8: Advanced Eigendecomposition

2022-01-18

저번 포스팅에 고유값(eigenvalue), 고유벡터(eigenvector), 대각행렬(diagonal matrix) ,대각화(diagonalization)를 활용하여 n차 정방행렬의 p제곱을 구하였고, 이번에는 EVD(Eigenvalue-eigenvector Decomposition)에 대한 수업을 진행하였다. EVD는 n by n 정방행렬에 대해서만 적용이 가능하고 Markov process 과정을 적용하여 계산하였다.

• Symmetric Matrix If Matrix A is symmetric, then any two eigenvectors from different eigenspaces are orthogonal.

  

  

  An n x n matrix A is said to be orthogonally diagonalizable.

• ex) Markov Process

  

  

  

  step 1) eigenvalue 구하기

  

  step 2) eigenvector 구하기

  

  

  

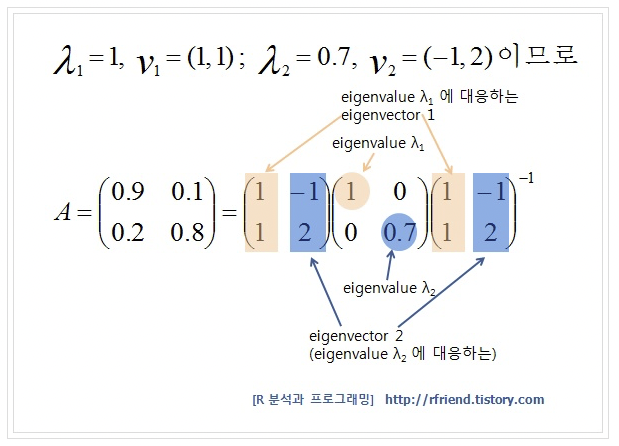
  step 3) RESULT

  

본 그림의 출처는 아래와 같음.

R 분석과 프로그래밍