goormNLP [Linear Algebra & System]

Auspice by Goorm, Manage by DAVIAN @ KAIST

2022-01-10 (월)

머신러닝과 선형대수의 관계

2주차에는 머신/딥러닝에 들어가기에 앞서 Linear Algebra: 선형대수학에 대해서 수업을 진행하였다.

선형대수학은 연립방정식을 손쉽게 풀고자하는 고민으로부터 시작되었다. 머신러닝은 본질적으로는 컴퓨터가 이해할 수 있는 대량의 데이터. 즉 숫자를 이용해 복잡한 계산을 수행하는 것이므로 선형대수학의 수식과 계산 기법을 사용하면 최소한의 타이핑 만으로도 대량의 계산을 손쉽게 컴퓨터에게 지시하는 것이 가능해진다.

Lecture 1: Elements In Linear Algebra

Scalar, Vector, Matrix

1. Scalar: a single number.
2. Vector: an ordered list of numbers.
3. Matrix: a two-dimensional array of numbers.
   • Matrix size: 3 x 2 means [3 rows(행) and 2 columns(열)]
   • Row vector: a horizontal vector - 수평
   • Column vector: a vertical vector - 수직

• a vector of n-dimension is usually a column vector. a matrix of the size n x 1

• a row vector is usually written as its transpose.

• Square matrix ( # rows = # columns ).

• Rectangular matrix ( # rows != columns ).

• A^T: Transpose of matrix ( mirroring across the main diagonal ).

• A_2,1 = 3 => ( i , j )-th component of A.
• A_2,: = [3 4] => i-th row vector of A.

---

Vector/Matrix Add & Mul

• C = A + B : Element-wise addition.

• cA : Scalar multiple of vector/matrix.

• C = AB : matrix-matrix multiplication

• AB != BA : Matrix multiplication is NOT commutative.

---

Other Properties.

1. A(B+C) = AB + AC : Distributive
2. A(BC) = (AB)C : Associative
3. (AB)^T = B^TA^T : Property of transpose

---

Lecture 2: Linear System

• A linear equation in the variables x1, …, x_n is an equation that can be written in the form.

a1x1 + a2x2+ ... + anxn = b

• The above equation can be written as a^Tx = b

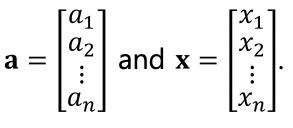
• A system of linear equations (or a linear system) is a collection of one or more linear equations involving the same variables.

X1, ..., Xn.

Linear system example

• we solve for x₁, x₂, x₃ given a new person with his/her Weight, Height, Is_smoking. we can predict his/her life-span.

Step 1. Let’s collect all the coefficients on the left and form a matrix.

Step 2. Let’s form two vectors:

=> Multiple equations can be converted into a single matrix equations.

---

Identity Matrix

• Definition : An identity matrix is a square matrix whose diagonal entries are all 1’s, and all the other entries are zeros.
• Often, we denote it as

Inverse Matrix

• Definition : For a square matrix, its inverse matrix A^-1 is defined such that A^-1A = AA^-1 = I_n

• For a 2 x 2 matrix, its inverse matrix A^-1 is defined as

• We can now solve Ax = b as follows:

---

Step 4. Solving linear system via inverse matrix.

• Now, the life-span can be written as

  (life - span) = -0.4 * (Weight) + 20 * (Height) -20 * (Is_smoking).

---

Non-Invertible Matrix

if A is invertible, the solution is uniquely obtained as x = A^-1b.

if A is NOT invertible, the inverse does not exist?

*det A ** determines whether A is invertible *(when det A != 0) or not (when det A = 0).

=> if A is non-invertible, Ax = b will have either no solutuon or infinitely many solutions.

---

Rectangular Matrix A in Ax = b